Quantization in Deep Learning

Quantization

Quantization in deep learning refers to the process of reducing the precision of the weights and activations of a neural network, typically from 32-bit floating-point numbers to lower bit-width integers. This can significantly reduce the memory requirements and computational complexity of neural networks, making them more efficient for deployment on resource-constrained devices. In this blog, I'll outline several major strategies in quantization for deep learning, including the types of quantization, special data structures for quantization and techniques used.

Strategies

1. Learned Quantization Schemes

   • Instead of using fixed quantization schemes, learned quantization allows the network to adaptively determine the quantization parameters during training.
   • Benefits:
     • Improved flexibility: The network can learn the most suitable quantization parameters.
     • Better adaptation to data distribution: Learned quantization can adjust to the characteristics of the data.
   • Challenges:
     • Increased training complexity: Learning quantization parameters adds complexity to the training process.
   • A popular use case: Dynamic (Range) Quantization
     • Focuses on adjusting quantization parameters based on the observed dynamic range
     • Available during training and inference
     • int8: quantized_val = real_value* scaling_factor + zero-point,
     • zero-point is the int8 value corresponding to the value 0 in the float32 realm, scaling_factor = 127 / max_val_in_tensor
     • float32 values outside of the [a, b] range are clipped to the closest representable value
     • activations are read and written to memory in floating point format

2. Post Training Static Quantization

   • key: Unlike constant tensors such as weights and biases, variable tensors such as model input, activations (outputs of intermediate layers) and model output cannot be calibrated unless we run a few inference cycles.
   • allows both arithmetic and int8 memory access
   • feed batches of data through the network and compute distributions of different activations -> observer task
   • the distributions determine how the activations are quantized (e.g. equal distributed 256 values) at inference time
   • Operator fusion: fuse multiple operations to a single operation, saving memory access and numerical acuracy
   • per-channel quantization: independely quantize weights in each output channel (or other specific dimensions) in a conv/linear layer -> higher accuracy but more memory usage
   • Benefits:
     • Simplicity: Can be applied to pre-existing models without the need for retraining.
     • Quick deployment: Pre-trained models can be quantized for efficient deployment.
     • Reduce latency a lot (don't have to convert to quantized values to float and convert back between operations)
   • Challenges:
     • Loss of accuracy: Post-training quantization may lead to a significant drop in model accuracy.

3. Quantization Aware Training

   • This strategy involves training the neural network with quantization in mind. During training, the model is exposed to the quantization effects, helping it adapt to lower precision.
   • highest accuracy typically, as it considers during training methods that rectify inference quantization errors
   • weights and activations are “fake quantized” during training (both forward and backward)
   • quantization-aware loss encourages the model to minimize the difference between quantized values (e.g., 8-bit integers) and the original (unquantized) values.
   • Fake quantization layer: layers that mimic quantization and dequantization operations. During training, gradients flow through the fake quantization layers. This means that the model learns how to deal with the discrete values introduced by quantization.

Guideline

The developer team of Tensorflow has created a suggested workflow for quantization as follows, which makes a lot of sense and should be considered as a viable chain of thoughts when applying quantization:

1. try default Dynamic
2.
	2.1 if (fast enough) go to 3
	2.2 else: use static quantization
3.
	3.1. if (no evaluation or equivalently, is training): use quantization-aware training
	3.2. else: done

Mixed Precision Training

Mixed-precision quantization involves using different precision levels for different layers of the neural network. For example, weights may be quantized to 8 bits, while certain layers or activations may use higher precision. While some consider it as part of the quantization, I'd personally treat it as a separate concept as it takes up an important component in many of the large model trainings, which preserving the accuracy to a large extent using a master copy in higher precision.

Major steps

1. Intuition: FP32 -> FP16 during forward pass (model now in FP16) and FP16 -> FP32 during back-prop (to ensure accuracy)
2. A master copy of the weights is stored in FP32. This is converted into FP16 during part of each training iteration (one forward pass, back-propagation and weight update). At the end of the iteration, the weight gradients are used to update the master weights during the optimizer step.
3. For FP16, any number with magnitude smaller than will be equated to zero as it cannot be represented (this is the denormalized limit for FP16). Therefore, by completing the updates in FP32, these update values can be preserved.
4. Loss Scaling: small gradient values can appear even before update -> in range of
   • fix: after model forward pass, loss is calculated, we then do a scaling to ensure gradient values are greater than
   • weights in FP16 now -> [[loss in FP32 -> Scaled loss in FP32 -> Scaled Gradients in FP16]]
   • Afterwards, scaled gradient in FP32 -> gradient in FP32
   • Loss function is FP32 operation to preserve error accuracy, hence the loss always in FP32
   • Note: large scaling factor is okay except when it causes overflow (remove scaler in this case): generally 500,000 to 10,000,000
   • automatic scaling: start with very large ,
     1. if Inf or NaN present, decrease scale, skip update.
     2. If Inf or NaN missing for while, increase the scale

A great illustration of the steps outlined above is here (source: Nvidia):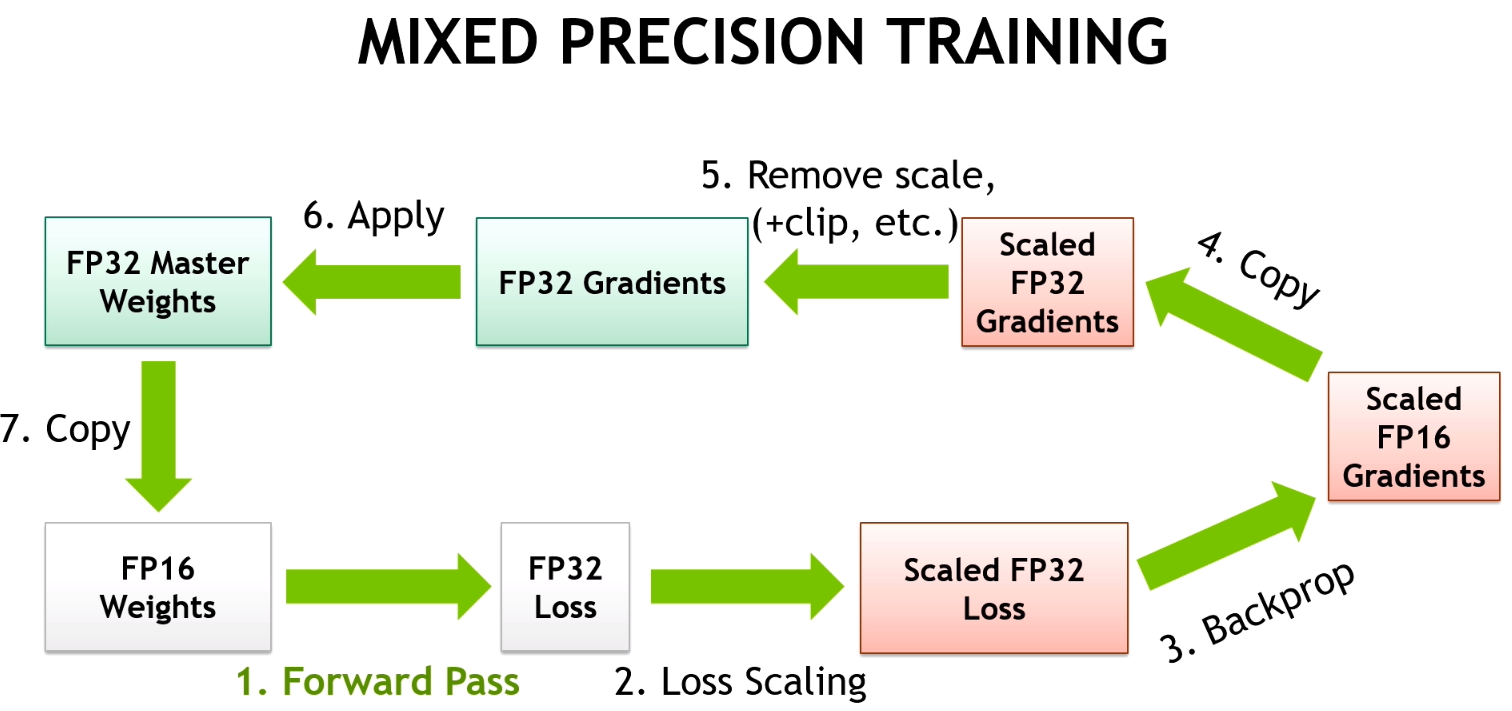

In some cases, reduction from FP32 into FP16 can result in too significant accuracy losses. Hence researchers have explored alternative data structures like Bfloat16 aned NF4 to help resolve this issue. So in the final section of this blog, let me give a short overview of these data types to make the topic of quantization complete and sound.

Sample Code

I'll provide a simple illustration of python code for each strategy using torch.quantization library

import torch
import torchvision.transforms as transforms
import torchvision.models as models
import torch.quantization as quantization

# Load a pre-trained model
model = models.resnet18(pretrained=True)
model.eval()

# Define example input data
example_input = torch.rand(1, 3, 224, 224)

# ------------------------------
# Dynamic (Range) Quantization
# ------------------------------

quantized_model_dynamic = quantization.quantize_dynamic(
    model,  # Original model
    {torch.nn.Linear},  # Specify layers to quantize
    dtype=torch.qint8  # Quantization data type
)
quantized_model_dynamic.eval()

# ------------------------------
# Post Training Static Quantization
# ------------------------------

quantized_model_static = quantization.quantize_qat(
    model,  # Original model
    {torch.nn.Linear},  # Specify layers to quantize
    input_calibrations=[(example_input, 0)],  # Calibration data
    dtype=torch.qint8  # Quantization data type
)
quantized_model_static.eval()

# ------------------------------
# Quantization Aware Training
# ------------------------------

# Define a dummy dataset loader for quantization-aware training
dummy_data_loader = torch.utils.data.DataLoader(torch.randn(100, 3, 224, 224))

# Enable quantization-aware training
quantized_model_qat = quantization.QuantWrapper(model)
quantized_model_qat.train()

# Fine-tune the quantized model
for epoch in range(5):
    for data, target in dummy_data_loader:
        quantized_model_qat.zero_grad()
        output = quantized_model_qat(data)
        loss = torch.nn.functional.cross_entropy(output, target)
        loss.backward()
        # Perform optimization steps
        ...

# ------------------------------
# Mixed Precision Training
# ------------------------------

# Convert the model to mixed precision
mixed_precision_model = quantization.quantize_jit(
    model,  # Original model
    example_input,  # Example input for calibration
    dtype=torch.float16  # Quantization data type
)

# Use mixed precision model for training
mixed_precision_model.train()

DL-specific Data structure

Bfloat16

Bfloat16 (Brain Floating Point 16-bit) was developed by Google as part of its efforts to optimize deep learning performance.It plays a role in quantization by offering reduced precision suitable for deep learning applications. Its use in mixed-precision training and compatibility with specific hardware accelerators contribute to improved efficiency in terms of both computation and memory usage.

• Motivation:
  • Ensure identical behavior for underflows, overflows, and NaNs -> bfloat16 has the same exponent size as FP32.
  • However, bfloat16 handles denormals differently from FP32: it flushes them to zero.
  • Unlike FP16, which typically requires special handling via techniques such as loss scaling, BF16 comes close to being a drop-in replacement for FP32 when training and running deep neural networks.

4-bit NormalFloat (NF4)

4-bit quantization is discussed in the popular paper QLoRA: Efficient Finetuning of Quantized LLMs. The aim is to reduce the memory usage of the model parameters by using lower precision types than full (float32) or half (bfloat16) precision.

• Normalization: standard normalize the weights
• Method: Find nearest value in evenly spaced [-1, 1] ranged values. e.g. [-1, -.5, 0, .5, 1] -> 0.32 is quantized to .5
  • Double Quantization: - A method that quantizes the quantization constraints saving additional memory (approx. 3 GB for a 65B model).
  • DQ symmetrical quantizes the 32-bit Floating Point (FP32) quantization constants of the first quantization into 8-bit Floating Point (FP8) quantized quantization constants.